Algorithms for Multiplying and Dividing Whole Numbers

In this section we will discuss several algorithms for multiplying and dividing whole numbers.

Multiplication:

• For small numbers we can physically represent multiplication as repeated addition with units, strips,
and squares. Whenever we reach ten of one kind of manipulative piece we should exchange. 10
units → 1 strip, 10 strips → 1 mat, 10 mats → one cube,...

• For larger numbers place value cards are a reasonable model. To use place value cards we will
take advantage of the distributive property.

1. Example: 5 ·147

Mark off a card with squares for ones, tens, hundreds,... We will record all of our multiplication
on this card.

5 ×147 = 5(100 + 40 + 7) = 5 ·100 + 5 · 40 + 5 · 7 = 5(100) + 20(10) + 35

So we record 35 ones, 20 tens and 5 100s. Then begining in the ones square we make exchanges
so that there are no more than 9 markers in any square.

Here we’ll trade 30 for 3 tens. This gives us 23 tens and so we’ll trade 20 of them for 2
hundreds.

2. The instructional algorithm is:

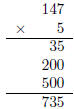
3. The final alogrithm is:

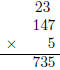
• For larger numbers the models become complicated so we present only the instructional and final
algorithm.

Example: Compute 16× 321.

– Expanded notation:

– Instructional Algortihm

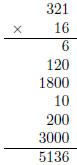
– Final Algorithm: standard multiplication algortihm for multi-digit numbers.

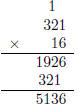
Division:

• Theorem: (The division algortihm) If a and b are whole numbers with b not zero, there exists
exactly one pair of whole numbers q and r with 0 ≤ r ≤ q such that a = b · q +r. The number q is
the quotient and the number r is the remainder of a divided by b.

• For small numbers we know a variety of methods to compute a ÷ b. For large numbers, however,
these methods become unmanagable. We need a procedure for large numbers and this procedure
is called long division.

• Long division is really just repeated subtraction. For example compute 1000 ÷ 9 by repeated
subtraction. First subtract 100 9's or 900 from 1000. This leaves 100. Take 10 9's from 100 to get
10. Take one more nine to get 1. In total, we subtracted 9, 111 times from 1000 with a remainder
of 1. So our answer is 111 R 1. To check this answer we plug our result into the division algorithm
formula. 1000 = 111 · 9 + 1:

The scaffold algorithm is a systematic framework for organizing computations like the above.

• Scaffold algorithm for 1000 ÷ 9.

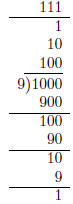
Since 0 ≤1 < 9 our answer is 111 R 1.

• Scaffold algorithm for long division.

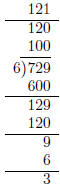
Since 0 ≤ 3 ≤ 6 we stop and our answer is 121 R 3.

• The scaffold alogirthm is now standard among elementary teachers. There is a notationally compact
alogrithm which you may be familiar with, however. This method saves a little writting but
unfortunately tends to obscure what’s actually going on. The compressed algortihm:

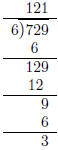
You can see that there’s a lot left out of this algorithm and when students learn and practice the
notionally compact form they are likely to lose sight of what division is really all about: repeated
subtractions.

• Here’s another example with the scaffold algorithm. Compute 32516 ÷ 312.

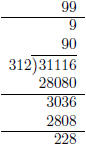
Since 0 ≤ 228 < 312 we stop and our answer is 99 R 228.

• If the divisor is a single digit there is a simple procedure to compute a ÷ b. The procedure is called
the short division alogrithm. You can see an example in the text, p. 192.