Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Math Worksheet

1.
(a) State the definition of a one-to-one function.

(b) State the definition of an inverse function.

2. Determine whether the following functions are one-to-one.

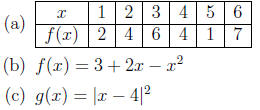
3. If f is a one-to-one function such that f(2) = 9, what is f^-1(1)?

4. If 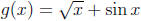,find f^-1(1)

5. find a formula for the inverse of a function. Sketch the graphs of the function and its
inverse and verify that you have found the inverse correctly.

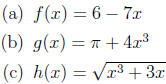
6. Find

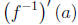
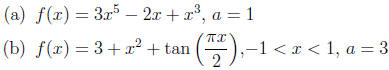
7.
(a) If we shift a curve to the left, what happens to its reflection about the line y = x?
In view of this geometric principle, find an expression for the inverse of g (x) =
f (x + c), where f is a one-to-one function.

(b) Find an expression for the inverse of h (x) = f (c x), where c ≠ 0

8. (a) If f is a one-to-one, twice differentiable function with inverse function g, show
that

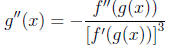
(b) Deduce that if f is increasing and concave upward, then its inverse function is
concave downward.

9. Recall the following theorem from the text.

Theorem. If f is a one-to-one differentiable function with inverse function g = f^-1
and 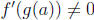, then the inverse function is differentiable at a and

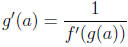
The purpose of this problem is to guide you through the proof of this theorem.

(a) State the definition of the derivative of g at the point x = a.

(b) Using the definition of an inverse function and that g (x) = y, g (a) = b find f (y)
and f (b).

(c) Rewrite the definition from part (a) using the notation in part (b).

(d) Why is g = f^-1 continuous? So, if x→a then g (x)→?

(e) Use the limit laws to recognize that

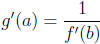
(f) Finally, use the notation of part (b) to rewrite the result obtained in (e) to get
the desired result.